Exploratory Data Analysis¶
from IPython.display import HTML
HTML('''<script>
code_show=true;
function code_toggle() {
if (code_show){
$('div.input').hide();
} else {
$('div.input').show();
}
code_show = !code_show
}
$( document ).ready(code_toggle);
</script>
The raw code for this IPython notebook is by default hidden for easier reading.
To toggle on/off the raw code, click <a href="javascript:code_toggle()">here</a>.''')
Project Introduction¶
We are asked to predict bandgap and formation energy for transparent conductors. Two types of data are given: crystal structure and atomic geometry. Training set is 2400 with values of bandgap and formation energy labeled, so it is a supervised learning and regression problem. Test set is 600. Dataset is not big.
import pandas as pd
import numpy as np
from matplotlib import pyplot as plt
import seaborn as sns
from pymatgen.core import periodic_table
train = pd.read_csv('train.csv')
test = pd.read_csv('test.csv')
print('Train info')
train.info()
print('Test info')
test.info()
print('Train describe')
train.describe()
print('Test describe')
test.describe()
print('Train head')
train.head()
Inspect geometry file for id = 1¶
finp = open('train/1/geometry.xyz').readlines()
#finp = pd.read_csv('train/1/geometry.xyz')
#print(*finp[:]) # File truncated to save space
print('(File truncated to save space)')
The total number of atoms includes O, whereas the percentage of Al, Ga, In sums up to 1 and does not include O!
#missing data
print('Missing train values = ',train.isnull().values.sum())
print('Missing test values = ',test.isnull().values.sum())
Bandgap and Formation Energy¶
train.bandgap_energy_ev.hist(bins=50)
plt.xlabel('bandgap')
#train.bandgap_energy_ev.plot.density()
plt.xlim(0,6)
plt.show()
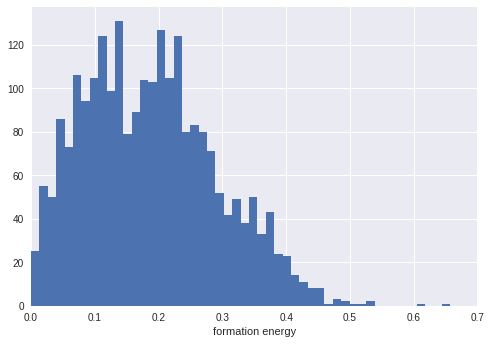
train.formation_energy_ev_natom.hist(bins=50)
plt.xlabel('formation energy')
#train.formation_energy_ev_natom.plot.density()
plt.xlim(0,0.7)
plt.show()
Bandgap and Formation energy both behave like normal distribution, where the range of bandgap is from 0 to ~5 eV, and formation from 0 to ~0.5 eV.
Spacegroup¶
train.spacegroup.value_counts()
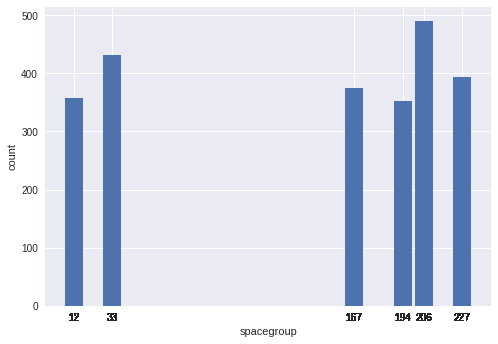
plt.bar(train.spacegroup.value_counts().index.values,train.spacegroup.value_counts(),width=10)
plt.xlabel('spacegroup')
plt.ylabel('count')
plt.xticks(train.spacegroup)
plt.show()
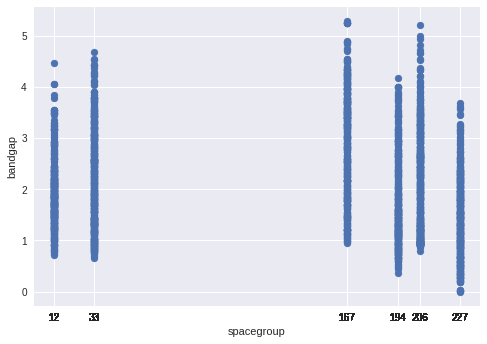
plt.scatter(train.spacegroup,train.bandgap_energy_ev)
plt.xlabel('spacegroup')
plt.ylabel('bandgap')
plt.xticks(train.spacegroup)
plt.show()
Looks like there's only 6 spacegroups and are distributed almost equally within the training set. SGs can be distinguished from each other, eg. 227 gives lower bandgap than the rest.
N total atoms¶
#train.number_of_total_atoms.hist(bins=100)
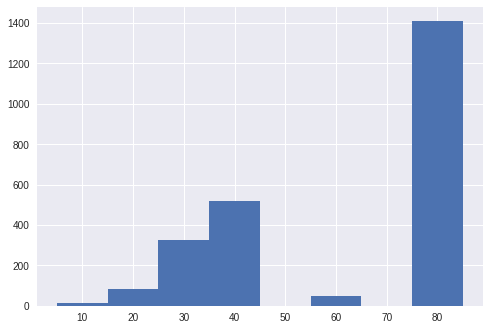
plt.bar(train.number_of_total_atoms.value_counts().index.values,train.number_of_total_atoms.value_counts(),width=10)
plt.show()
Number of total atoms take on discrete values, from 10 to 80, but not 50 and 70. Most data sets have 80 atoms.
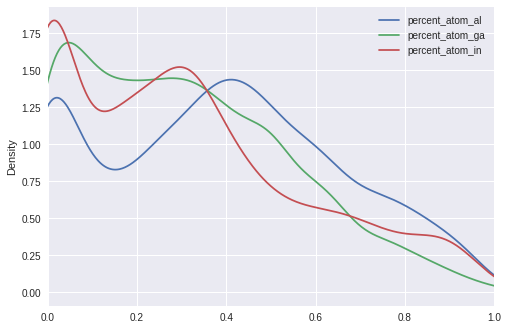
Percentage of Al, Ga, In¶
train.percent_atom_al.plot.density()
train.percent_atom_ga.plot.density()
train.percent_atom_in.plot.density()
plt.xlim(0,1)
plt.legend()
plt.show()
Al and Ga have two peaks, around 0 and 0.3-0.5, whereas most data has only 0.1 In.
print('Sum of percent of Al, Ga, In = ',train.percent_atom_al.values[0]+train.percent_atom_ga.values[0]+train.percent_atom_in.values[0])
As pointed out earlier, total number of atom includes O, which is not included in the percent of Al, Ga, In.
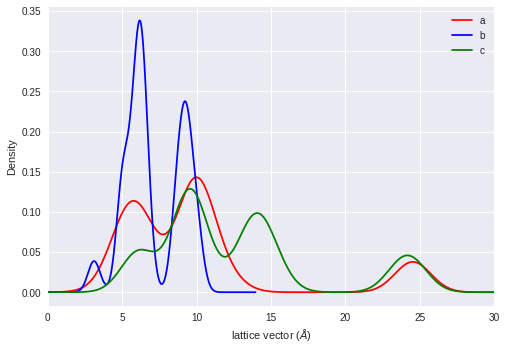
Lattice vectors and angles¶
#train.lattice_vector_1_ang.hist(bins=100)
train.lattice_vector_1_ang.plot.density(color='red')
train.lattice_vector_2_ang.plot.density(color='blue')
train.lattice_vector_3_ang.plot.density(color='green')
plt.legend(['a','b','c'])
plt.xlabel('lattice vector ($\AA$)')
plt.xlim(0,30)
plt.show()
Lattice a, b, c are unique. Lattice b is less than 10 A, and most frequent values are around 5 A and 10 A. Lattice a and c can go up to 25 A.
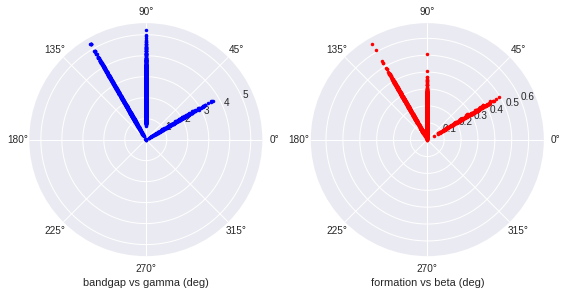
#alpha
plt.subplot(121,polar=True)
plt.polar(np.deg2rad(train.lattice_angle_alpha_degree),train.bandgap_energy_ev,'b.')
plt.xlabel('bandgap vs alpha (deg)')
plt.subplot(122,polar=True)
plt.polar(np.deg2rad(train.lattice_angle_alpha_degree),train.formation_energy_ev_natom,'r.')
plt.xlabel('formation vs alpha (deg)')
plt.tight_layout()
plt.show()
#beta
plt.subplot(121,polar=True)
plt.polar(np.deg2rad(train.lattice_angle_beta_degree),train.bandgap_energy_ev,'b.')
plt.xlabel('bandgap vs beta (deg)')
plt.subplot(122,polar=True)
plt.polar(np.deg2rad(train.lattice_angle_beta_degree),train.formation_energy_ev_natom,'r.')
plt.xlabel('formation vs beta (deg)')
plt.tight_layout()
plt.show()
#gamma
plt.subplot(1,2,1,polar=True)
plt.polar(np.deg2rad(train.lattice_angle_gamma_degree),train.bandgap_energy_ev,'b.')
plt.xlabel('bandgap vs gamma (deg)')
plt.subplot(1,2,2,polar=True)
plt.polar(np.deg2rad(train.lattice_angle_gamma_degree),train.formation_energy_ev_natom,'r.')
plt.xlabel('formation vs beta (deg)')
plt.tight_layout()
plt.show()
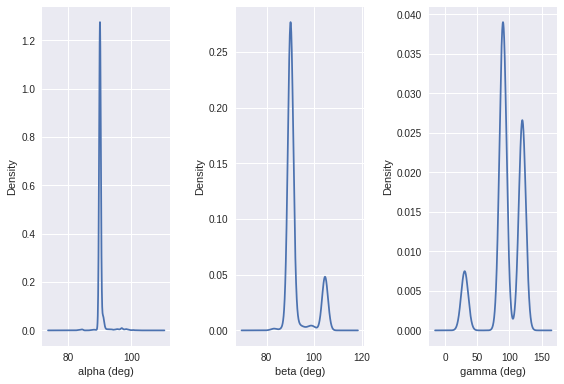
plt.subplot(131)
train.lattice_angle_alpha_degree.plot.density()
plt.xlabel('alpha (deg)')
plt.subplot(132)
train.lattice_angle_beta_degree.plot.density()
plt.xlabel('beta (deg)')
plt.subplot(133)
train.lattice_angle_gamma_degree.plot.density()
plt.xlabel('gamma (deg)')
plt.tight_layout()
plt.show()
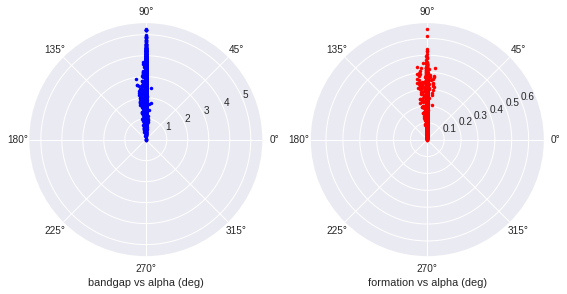
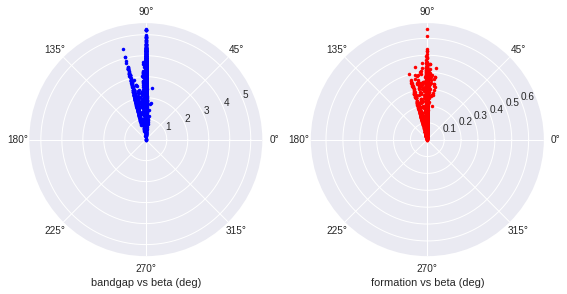
The angles seems to be discretized. Alpha is always 90 deg, beta is mostly 90 deg, sometimes 105 deg due to the restricted spacegroup. Gamma can take 30 deg, 90 deg and 120 deg.
Feature Correlation¶
train.corr()
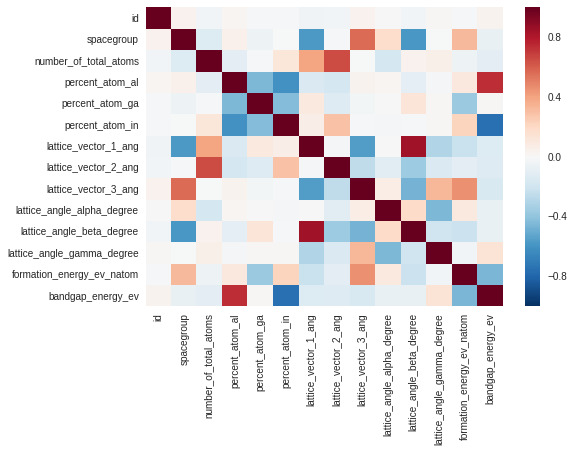
Let's visualize in a heat map.
#plt.imshow(train.corr(),cmap='hot')
#plt.matshow(train.corr(),cmap='hot')
#plt.colorbar()
sns.heatmap(train.corr())
plt.show()
Bandgap has strong positive correlation with percent of Al, strong negative correlation with percent of In, and no correlation with percent of Ga. Formation energy is weakly (~0.4) correlated with lattice c and percent of Ga. Bandgap and formation energy are also somewhat correlated with each other.
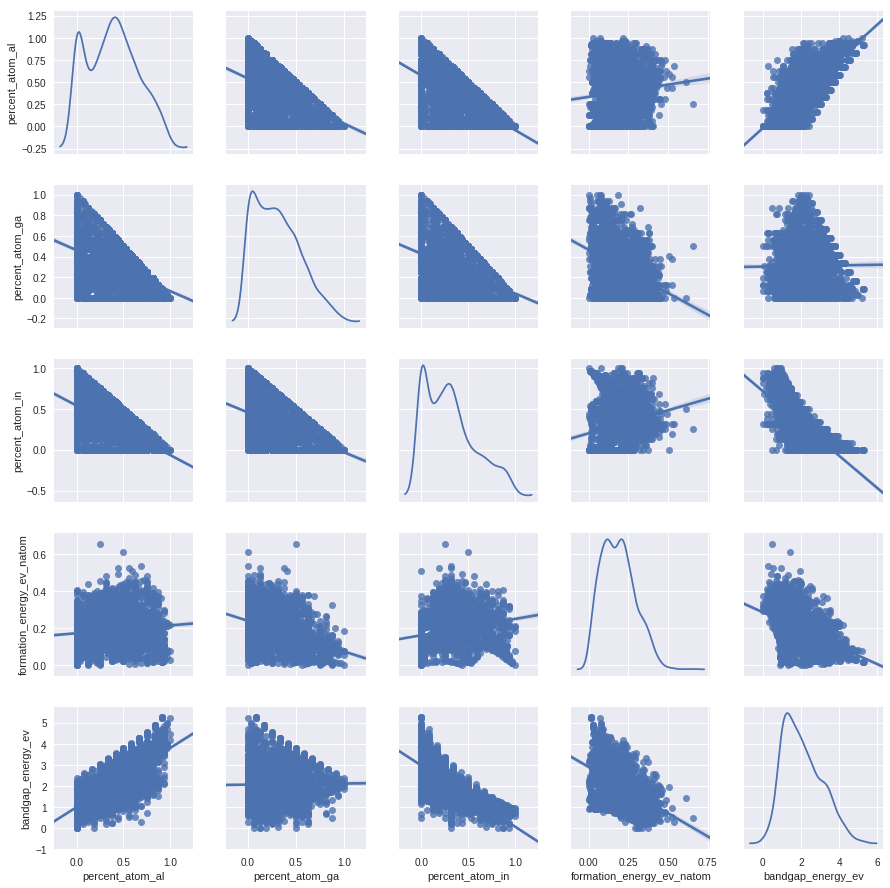
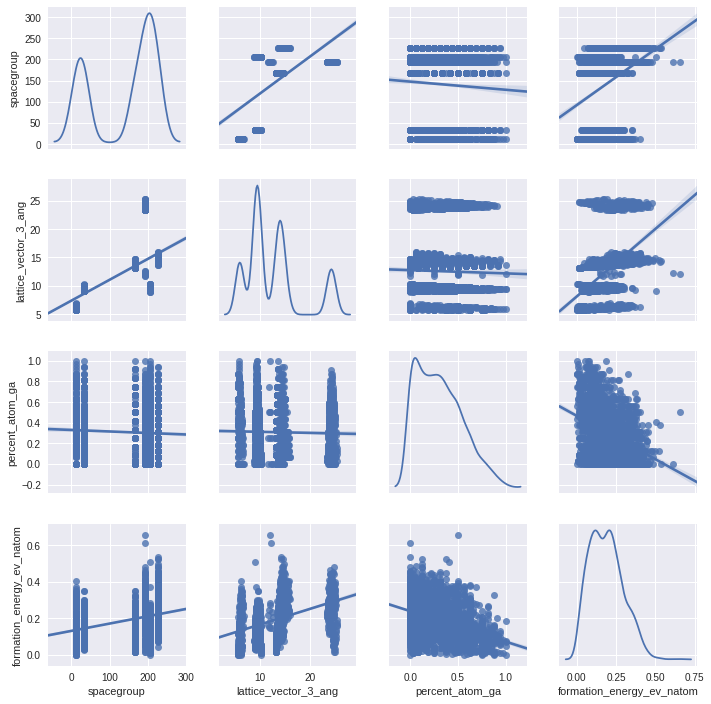
sns.pairplot(train,vars=['percent_atom_al','percent_atom_ga','percent_atom_in','formation_energy_ev_natom','bandgap_energy_ev'],kind='reg',diag_kind='kde')
plt.show()
The scatter plots agree with the correlation strength.
sns.pairplot(train,vars=['spacegroup','lattice_vector_3_ang','percent_atom_ga','formation_energy_ev_natom'],kind='reg',diag_kind='kde')
plt.show()
Eventhough the spacegroup, lattice c and percent of Ga shows some correlation with the formation energy, the regression doesn't fit too well.
New feature generation: Volume¶
def get_vol(a,b,c,alpha,beta,gamma):
vol = a*b*c*np.sqrt(1+2*np.cos(np.deg2rad(alpha))*np.cos(np.deg2rad(beta))*np.cos(np.deg2rad(gamma))-np.cos(np.deg2rad(alpha))**2-np.cos(np.deg2rad(beta))**2-np.cos(np.deg2rad(gamma))**2)
return vol
train['vol'] = get_vol(train.lattice_vector_1_ang,train.lattice_vector_2_ang,train.lattice_vector_3_ang,train.lattice_angle_alpha_degree,train.lattice_angle_beta_degree,train.lattice_angle_gamma_degree)
test['vol'] = get_vol(test.lattice_vector_1_ang,test.lattice_vector_2_ang,test.lattice_vector_3_ang,test.lattice_angle_alpha_degree,test.lattice_angle_beta_degree,test.lattice_angle_gamma_degree)
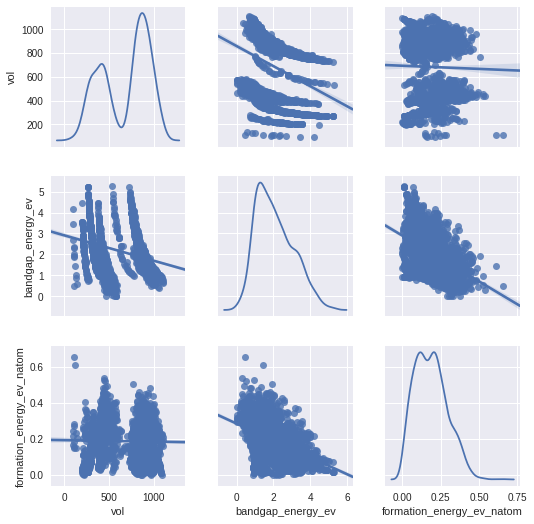
sns.pairplot(train,vars=['vol','bandgap_energy_ev','formation_energy_ev_natom'],kind='reg',diag_kind='kde')
plt.show()
Vol, a new feature generated from lattice, show some correlation with bandgap and formation energy.
New feature generation: Total Mass of Al, Ga, In¶
def get_n_atom(df,df_name):
N_Ga = []
N_Al = []
N_In = []
N_O = []
for i in df.id:
n_Ga = 0
n_Al = 0
n_In = 0
n_O = 0
with open(str(df_name) + '/' + str(i) + '/geometry.xyz','r') as finp:
for line in finp:
if line.split()[0] == 'atom':
if line.split()[4] == 'Ga':
n_Ga += 1
elif line.split()[4] == 'Al':
n_Al += 1
elif line.split()[4] == 'In':
n_In += 1
elif line.split()[4] == 'O':
n_O += 1
N_Ga.append(n_Ga)
N_Al.append(n_Al)
N_In.append(n_In)
N_O.append(n_O)
df['n_ga'] = pd.DataFrame(N_Ga)
df['n_al'] = pd.DataFrame(N_Al)
df['n_in'] = pd.DataFrame(N_In)
df['n_o'] = pd.DataFrame(N_O)
return df['n_al'], df['n_ga'], df['n_in'], df['n_o']
def get_mass(df):
mass_ga = periodic_table.Element['Ga'].atomic_mass
mass_al = periodic_table.Element['Al'].atomic_mass
mass_in = periodic_table.Element['In'].atomic_mass
mass_o = periodic_table.Element['O'].atomic_mass
tot_mass_ga = df['n_ga']*mass_ga
tot_mass_al = df['n_al']*mass_al
tot_mass_in = df['n_in']*mass_in
tot_mass_o = df['n_o']*mass_o
return tot_mass_al, tot_mass_ga, tot_mass_in, tot_mass_o
train.n_al, train.n_ga, train.n_in, train.n_o = get_n_atom(train,'train')
test.n_al, test.n_ga, test.n_in, test.n_o = get_n_atom(test,'test')
train['mass_al'], train['mass_ga'], train['mass_in'], train['mass_o'] = get_mass(train)
test['mass_al'], test['mass_ga'], test['mass_in'], test['mass_o'] = get_mass(test)
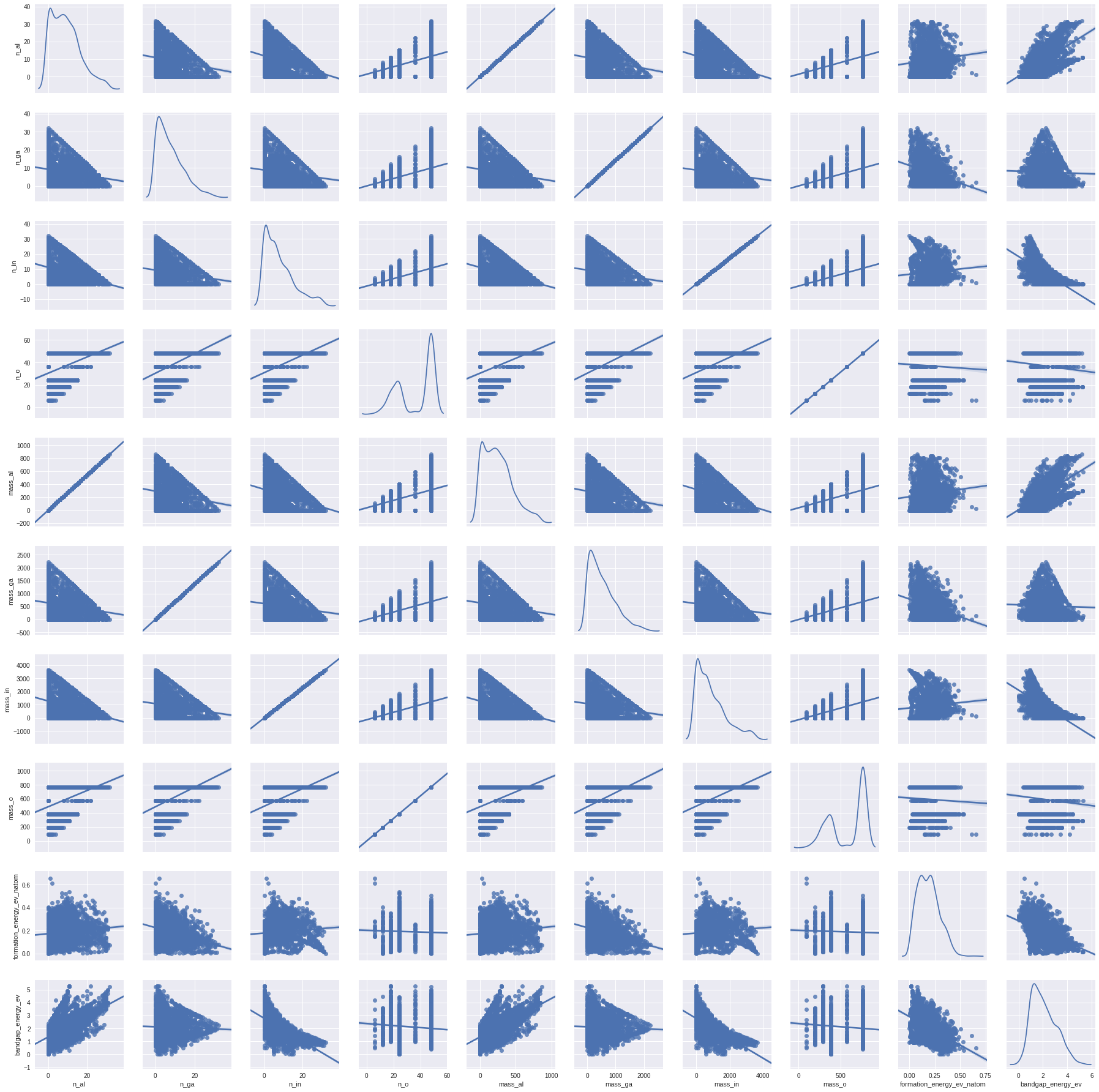
sns.pairplot(train,vars=['n_al','n_ga','n_in','n_o','mass_al','mass_ga','mass_in','mass_o','formation_energy_ev_natom','bandgap_energy_ev'],kind='reg',diag_kind='kde')
plt.show()
Al, Ga and In (except O) show good correlation with the bandgap and formation energy.